Домой! Оглавление Предисловие Теория Задачи
Задачи
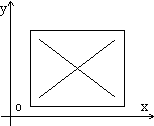
1. В четырехугольнике АBCD (рис.6) угол А больше угла B, угол B больше угла C, угол C больше угла D, а угол D больше угла A. Определить, какой из углов А и С больший, если известно, что линии магнитной индукции направлены за плоскость рисунка. Решение

2. Даны два камертона, первоначально одинаковых. Затем первый камертон погружают в смесь, содержащую чернозем и глинозем в соотношении 1:2. Сравните длины волн, создаваемых обоими камертонами после процедуры пачкания. Решение
3. Докажите, что натуральные логарифмы всех действительных чисел равны. Решение
4. Докажите, что в
произвольном треугольнике сумма
длин любых двух сторон равна длине
третьей стороны.
 Решение
Решение
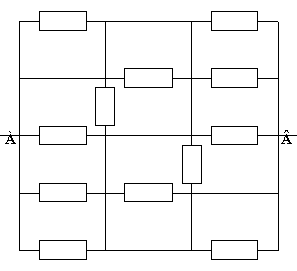
5. На рис.7 приведено множество точек координатной плоскости. Является ли данное множество графиком какой-либо функции и если да, то какой? Решение
6. (Задача Краснодарского ТЮФ-96). Русская пословица гласит: "Знал бы, где упасть, - соломки бы подстелил". Сколько нужно подстелить соломы, чтобы без опасения падать на нее? Решение
7. Проделайте и опишите опыт по получению гидроксида воды. Решение
8. Докажите, что все нечетные числа делятся на 2. Решение
9. (9-10 - Задачи из программы ЗМШ, Заочной Музыкальной Школы при училище им. Гнесиных). Концертный рояль "Красный Октябрь" водоизмещением V=0,5 м3 состоит из 10,52.1028 электронов, такого же количества протонов и 20.1027 нейтронов. Определите плотность шоколада. Землю считать абсолютно твердой. Решение
10. Рояль из предыдущей задачи закреплен в вертикальном положении на невесомой опоре, которая покоится на гладкой горизонтальной плоскости. За ним "сидит" пианист массой 65 кг и исполняет "Контрреволюционный этюд" Ф. Шопена. Определить, достаточно ли импульса, сообщенного опоре за время игры для достижения первой космической скорости. Решение
11. Около окружности описан а) квадрат б) правильный пятиугольник в) правильный шестиугольник. Чему равно число p в каждом из этих случаев? Решение
12. Упростите выражение:
(cosx+(siny+3)2-tg(x-y))20
(4x+84y)1995+32-ix2 + 10x+34y-log234
+....+.....+4(x-y)3
где y=-2+xi+ cos2x/131 Решение
13. Два студента-химика запихнули в ректификационную колонну декана собственного факультета и включили установку. Определить, что они обнаружили, когда через пару минут заглянули внутрь. Решение
14. При селекции орлов в первом поколении гибридов получены нормальные и двуглавые орлы в соотношении 1:3. Какие из них доминантные, а какие рецессивные? Решение
15. (Обобщение задачи 14) В секретной лаборатории выведены 1-, 2-, ..., n-главые орлы. Причем, их количества относятся как 2-1:2-2: ...:2-n. Найти КПД селекции, если для торжественного вылета на день Независимости России требуются только двуглавые орлы, а n->oo. Решение
16. Абсолютно неупругий шарик массы m налетает на не абсолютно упругую стенку массы M (M>>m). Найдите, сколько энергии выделится при ударе, если известно. что m=M. Решение
17. Возможен ли случай,
когда длины окружностей различны, а
их радиусы равны? Приведите пример.
Если невозможен, то хорошенько
перечитайте вводную статью
(несколько раз).
 Решение
Решение
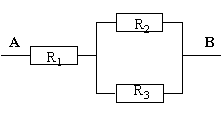
18. Определите напряжение между точками А и В в схеме на рис.8, если ток через А равен I. Сопротивление каждого резистора R. Решение
19. Два источника Э.Д.С. e1=4 В, e2=7 В закорочены накоротко. Различны ли токи короткого замыкания в этих случаях, если нет, то какой больше? Решение
20. Докажите, что через любые n точек пространства проходит прямая. Решение
21. Спортсмен, поднявшись на самолете на высоту 8848 м над уровнем моря, совершает прыжок с парашюта. Определите, сколько осталось жить спортсмену, считая с момента прыжка. Решение
22. Даны протон,
электрон, нейтрон и нейтрино.
Покажите, что невозможно
определить, какая из этих частиц
больше, если смотреть на них сзади.
 Решение
Решение
23. Напряжение между точками А и В в схеме на рис. 9 равно 7 В. Определите величину токов через R1, R2 и R3, если:
R2=3R1, R3=R1R2, R1=R3+4, про сопротивление проводов забыть. Решение
24. Докажите, что а)
любая прямая - это только частный
случай точки б) ромб - частный
случай квадрата.
 Решение
Решение
25. Теорема Синуса (по
имени ученого): если для
действительных или туфтовых чисел
Х, х выполняется неравенство
Х>>х, то верно также, что Х-х>>х.
Доказательство: Ну вычтем мы х
из Х. Что оно, сильно уменьшится?
Не противоречит ли теорема
основному неравенству туфтологии,
т.е. нет ли здесь парадокса? Решение
26. Докажите, что у любого действительного числа существует ненулевая мнимая часть. Решение
27. Решите уравнение: y2+8y=x-16. Решение
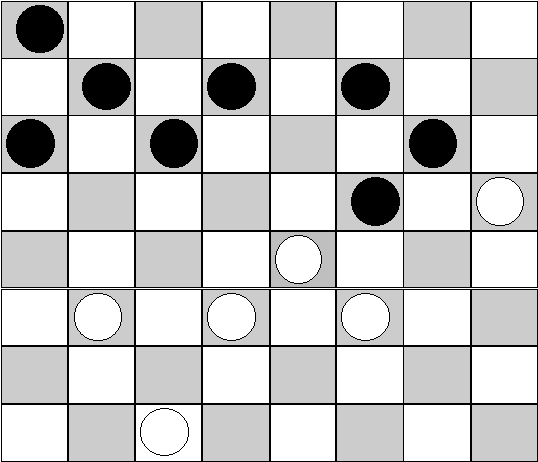
28. На рис. 10 приведена партия в шашки, ход черных. Имеет ли какой-либо из игроков беспроигрышную стратегию? Решение
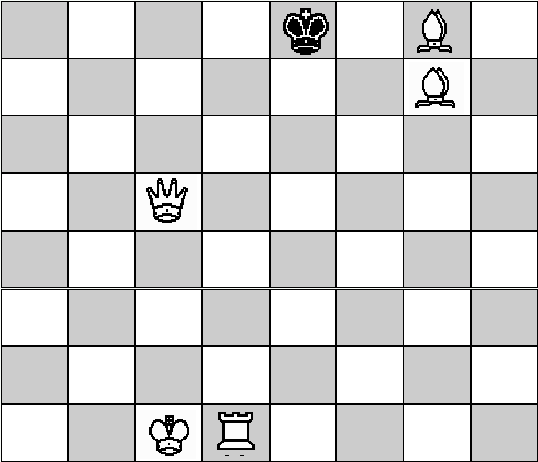
29. На рис. 11 приведена
шахматная позиция, ход белых.
Поставить мат в 33 хода.
 Решение
Решение
30. Верно ли утверждение, что любая директриса может делить углы точно пополам? Решение
31. Докажите, что задача N 19 не имеет решения, а приведенное решение - бред. Решение
32. Как можно получить вакуум из воды? Решение
33. Дано: физическое тело куда-то там летело. Определить, что находится в черном ящике. Решение
34. Докажите, что задача N 38 не имеет решения. Решение
35. Решить уравнение: x2+5zcosy+ylog2x+2zy=0 Решение
36. Карлсон, находясь на крыше, решил слетать к Малышу в окно. Определить, повезет ли Карлсону, если его пропеллер вращается с угловой скоростью 20 рад/c. Решение
37. Используя только кислород и водород получите вещество Н2О n способами. Решение
38. Докажите, что задача N 34 не имеет решения. Решение
39. Докажите, что в окружность можно вписать только равнобедренный треугольник. Решение