Теоретические сведения

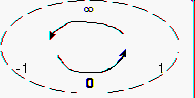
Домой! Оглавление Предисловие Теория Задачи

Теоретические сведения

1. Загрузка - предмет изучения туфтологии

2. Методы загрузки. Основное заблуждение туфтологии

1. Загрузка - предмет изучения туфтологии

1њ Загрузка есть особая форма материи, существующая в обратной зависимости от нас и нашего сознания. Т.е., чем больше сознания, тем меньше загрузки. Загрузку невозможно осязать. Ее материальность доказывается ее действием на человека.

2њ Загрузка является зарядом z-поля. Здесь и далее будем приближенно считать мозг человека пространством, заполненным упругими шариками-нейронами. При пронизывании мозга загрузочными линиями (1.5њ ) нейроны изменяют свое упорядоченное движение по окружностям вокруг оси симметрии мозга (т.н. осевая варка шариков) на хаотическое. Происходят их взаимные столкновения, во время которых на нейронах уравниваются электрические потенциалы, возникают микротоки. Под действием микротоков на нейронах выделяется загрузка. Явление возникновения загрузки под действием z-поля называется z-синтезом.

3њ Носителем загрузки называется несчастный, в мозгу которого происходит z-cинтез.

4њ Источником загрузки называется субъект, обладающий некоторым количеством загрузки. Источник загрузки индуцирует z-поле.

5њ Загрузочные линии - линии, соединяющие источника и носителя. Если z-линия не пересекает никаких препятствий (в основном, стены, дезагрузчики), а носитель находится вблизи источника, то происходит увеличение количества загрузки системы носитель-источник.

6њ Увеличение количества загрузки происходит по закону преумножения количества загрузки. Он гласит: количество загрузки, выделяющееся в системе, прямо пропорционально количеству алкоголя в крови носителя и обратно пропорционально квадрату расстояния между источником и носителем. Z = e _z^.Гњ /R² где Z- загрузка, ФБР
e _z - относительная дезагрузническая проницаемость, ед^-1
Гњ - градусная мера человека, град
R - расстояние, м

7њ Количество загрузки, выделяемой при гружении зависит от геометро-динамических характеристик мозга. Если нейроны имеют возможность летать по мозгу с большой скоростью, то их слишком мало. Если он трутся друг об друга, то часто сталкиваются, выделяя много загрузки. По определению: Z=U^.n^.cosa

где U - общее напряжение на при столкновении нейронов, В
n - нейронная концентрация, м^-3
cosa- косинус произвольного трехгранного угла; является геометрическим компонентом геометро-динамического показателя.

8њ Единица измерения загрузки ФБР. По закону преумножения, загрузка в 1 ФБР выделяется у некоего гениального носителя (e_z=1), если на каждый квадратный метр расстояния между ним и источником приходится 1 градус его опьянения. [Z] = 1 ФБР = 1 град / 1 м²

9њZ-поле также материально. Это доказывается тем, что скорость его распространения конечна. Последние измерения подтверждают, что скорость распространения z-поля равна скорости одного паровоза середины XIX века в системе единиц ПВП (Паровоз, Век, Парсек)

10њ Совокупность всех знаний о z-поле составляет единую теорию поля. Поскольку после распространения на некоторого человека z-поля, он начинает понимать, что никаких других полей (электромагнитных, гравитационных и прочих сильных и слабых) не существует. Значит все свойства z-поля являются едиными для всего множества полей.

11њ Принцип суперпозиции для z-полей: во время спора между источником и носителем, носитель всегда меняет свою позицию по данному вопросу на суперпозицию. Суперпозиции, обычно, сходны во всех случаях. Во общем случае ее можно сформулировать так: предмета обсуждения не существует, как и остального мироздания. Простой подстановкой предмета обсуждения получаем конкретную загрузку.

12њ На микроуровне загрузкой обладают туфтоны. Туфтон - это элементарная частица. Его размеры до сих пор неизвестны, т.к. как только его измеряют, он тут же уменьшается. Распространено мнение, что туфтон - это точка. На самом деле, туфтоны просто грузят своих исследователей. Другое название туфтона - гемоглобянин. Это единственная известная частица, обладающая собственным разумом. Масса покоя туфтона равна нулю, как и у квантов. Но, в отличие от последних, туфтоны все время покоятся. Свою инерцию они безвозмездно передали z-полю, которое обладает инерцией (туфтонов).

13њ При пересечении дезагрузчика загрузочной линией, появляется вихревое z-поле. Загрузочные линии "влетают" в одно ухо дезагрузчика, "вылетают" из другого и, возвращаясь назад к источнику, замыкаются. Возникновение вихревого поля сопровождается явлением самозагрузки источника.

Вопросы для самопроверки предназначены для того, чтобы выявить, загрузились вы уже или еще нет. Если вы согласны с данными в конце статьи ответами, то вам следует немедленно закрыть книгу и убрать подальше.

1. Книга является неодушевленным источником загрузки. Видите ли вы z-линии, исходящие из нее? (Оносительно верный ответ)

2. (притча ?2) Взбрело, как-то раз, Беллинсгаузену в голову уехать на месяц в Антарктиду, поохотиться на пингвинов. Он даже поссорился на этой почве с Лазаревым, который искренне считал, что охотиться на пингвинов - глупо. Помирились они только по возвращении Беллинсгаузена. Когда его поезд подъезжал к границам британской территории Вознесения, Лазарев уже стоял на перроне и кричал:"Старина! Сто лет тебя не видел!". Сколько дней а) в году б) в високосном году?

2. Методы загрузки. Основное заблуждение туфтологии

1њ Основное заблуждение опирается на то, что ни одна из современных наук не содержит положений, которые противоречили бы положениям какой-либо другой науки. Таким образом, не противоречит никакой науке и любая комбинация двух или более положений из различных областей. Это, безусловно, заблуждение. Основное заблуждения является достаточным, но обходимым условием для существования загрузки. Предпочтительным считается его обхождение при доказательстве.

2њ Цель туфтологии, как науки, доказать каждому человеку, что не существует ничего или что существует только точка.

3њ Сведением науки к точке называется такое доказательство, результатом которого является существование единственной точки и используются только положения данной науки. Наукой называется дисциплина, которую можно свести к точке. Пока удалось свести к точке только математику. Возможно лишение звания науки химии, т.к. не видно никаких путей, как свести химию к точке. Ее пока удалось свести только к 108 точкам (таблица элементов Д.И. Менделеева) и их количество может увеличиваться до бесконечности.

Пример 1 (притча 3). Дмитрий Иваныч Менделеев, земля ему пухом, был любителем всевозможных предсказаний и, откровенно говоря, суеверным человеком. Во всем видел он знамения будущего и мистические силы, даже в самых обычных и очевидных вещах. Возьмем хотя бы самую обыкновенную периодическую систему. Ведь Дмитрий Иваныч всем сказал, что она ему во сне привиделась. А на самом деле, шел он, однажды, по мостовой от Блока, которому бил морду, чтоб тот не приставал к Любушке Менделеевой, доченьке любимой. Да, на беду, по той же мостовой скакала кобыла Маруся, белая в яблоках, которую извозчик, мерзавец, третьи сутки гнилой соломой кормил. Тут, за черными мыслями, не заметили они друг друга. Причем, Маруся Дмитрия Иваныча больше не заметила, потому что упал он на ту самую мостовую, по которой совсем недавно шел. Затем мысли у него перемешались, а, точнее, упорядочились по периодам да по группам. И стал Менделеев смекать, как бы представить, будто все во сне свершилось. Дабы не смогли злые языки сказать, что яблоки на Ньютонов дважды не падают.

Проникшись сознанием значимости своего открытия и фатальностью расположения элементов по таблице, решил Дмитрий Иваныч, что содержится в его детище оракулская сила. В связи с чем, провозгласил новую науку - астрохимию. По которой выходит, что если человек родился в каком-то году, считая с начала века, то ему присущи химические свойства элемента из таблицы, у которого номер совпадает с этим годом рождения. Прогноз, составленный подобным образом, решено называть гироскопом. А календарь - Менделеевским. Все годы по Менделеевскому календарю переназначались, пока число элементов не достигло ста.

Для примера, гироскоп для 80-го года (из Большой Советской Энциклопедии). Ртуть (или просто Hydrargyrum). Серебристо-белый металл, жидкий при комнатной температуре. Принадлежит к весьма редким элементам, содержание в земной коре по массе 4,5^.10^-6%. Ядовит даже в малых количествах. При 4,155њК становится сверхпроводником. С кислородом (порядковый номер в системе 8) дает два соединения: черную закись и красную окись. В сухом воздухе неограниченно долго сохраняет свой блеск. Не растворяется в соляной кислоте, но растворима в царской водке. Химическая активность невелика.

К несчастью, Дмитрий Иваныч не успел придумать толкования гироскопов, так что толкуйте, как хотите. Заметим только, что последнее свойство означает, что мало кто из родившихся в 80-ом году станет химиком.

Пример 3. Очевидно, что некоторые силы (сила Лоренца, сила Архимеда, Ампера, Кориолиса и др.) не оправдывают своего названия. Так, например, сила Архимеда - это сила, которой обладал Архимед, сила Лоренца - Лоренц. Тем не менее, все они измеряются одной единицей - Ньютоном. Логически более обоснованно измерять соответствующую силу в соответствующих ученых. Для большей утилитарности, в Международной системе единиц "СИ++" за единицу силы, названной в честь ученого N принимается среднее значение силы давления, которую N оказывает на платформу, закрепленную под углом 0,19023 рад к горизонту, находясь в объеме керосина, к которому приливают и откачивают воду по гармоническому закону. Среднее значение фиксируется за четверть периода колебаний соотношения объемов воды и керосина. При этом сосуд, содержащий платформу, N и водный раствор керосина вращается в вертикальной плоскости с достаточным, чтобы удержать N на платформе, угловым ускорением. Именно поэтому, открытие принципиально новой силы для ученого, как правило, становится последним в жизни.

Зато теперь не возникает парадоксов, подобных этому: силу тока мы измеряем в Амперах, но силу Ампера в каких-то Ньютонах.

Задачки на смекалку.
1. Предложите, как можно сохранить за химией звание науки, не сводя ее к точке.
2. Зная о механическом, геометрическом смыслах производной, определите механический, геометрический, химический, туфтологический смыслы восьмерки. Ведь восьмерка, при определенном рассмотрении, - символ туфтологии.
3. Какая из тригонометрических функций является самой грязной и порочной?

3. Основное неравенство туфтологии

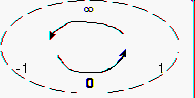
1њ Всякую прямую можно представить как окружность бесконечно большого радиуса. Выберем на некоторой числовой прямой (окружности) начало координат, единичный отрезок и направление "против часовой стрелки" как положительное (см. рис. 1).

2њ Линии любого рода на чертежах следует изображать пунктиром. Так как толщина и ширина каждой линии стремятся к нулю, а человеческий глаз не способен воспринимать настолько малые объекты, то все линии являются невидимыми. А из стереометрии известно, что невидимые линии изображаются пунктиром.

3њ При движении по числовой прямой в положительном направлении от х=-1 к х=1 получаем, что: 1>-1 Далее, при движении в том же направлении от х=1 через х=oo опять попадаем в точку х=-1; это означает, что: -1>1,

что следует из следующего свойства прямой: для a из R {x: x<a} образует луч с началом в точке а и направлением к +oo [a;+oo ).

Оба неравенства верны и означают для произвольных чисел х₁ и х₂, что x₁>x₂ тогда и только тогда, когда x₂>x₁. При сложении двух полученных неравенств получаем также верное неравенство: 0>0, или в общем случае: x<>x.

Последнее выражение называется основным неравенством туфтологии и означает, что некоторое число не равно самому себе ... н и к о г д а.

4њ Из феномена круговой сущности прямой следует, что не существует двух различных точек плюс и минус бесконечность, им эквивалентна единственная точка бесконечность, к которой можно стремится "слева" и "справа", как к нулю.

Тест на наивность

1. Является ли следующее доказательство верным: sin(5pi )=sin(7pi ) отсюда, 5pi =7pi , т.е. 5=7. Не правда ли? 2. Число 2 больше, чем 1 на 100%, а число 1 меньше, чем 2 на 50%. Это как, вообще?

4. Глюковое пространство

1њ Введем новое множество чисел, в котором имеет решение уравнение вида: 0^.х=с.

Решая уравнение, получим х=с/0=с , где (ту'фта) равна 1/0. Число, которое можно записать как z= ^.c, с из R, принадлежит множеству глюковых.

Справка. Названо в честь К.Глюка, австрийского композитора, разработавшего ТЧК (4.2њ ), мало смысля в математике. Впоследствии название получило более подходящее значение в русском языке, поскольку если уж числа bi, i²=(-1) - мнимые, то глюковые числа, действительно, глюковые.

Ту'фта - единственная буква атлантического алфавита. С ее помощью атланты могли выразить все, что чувствовали: обиду на остальному человечество, за то, что оно выкололо из прямой точку бесконечность (см 3.4њ ). Нижняя часть буквы ту'фты символизирует разорванную бесконечность, а верхняя (^. ) - вырванную из нижней части точку.

2њ Теория Числовых Комплексов (ТЧК) расширяет понятие о комплексных числах, т.е. повышает их комплексность. Согласно ТЧК комплексное число z в алгебраической форме имеет вид: z=a+bi+c .

3њ Глюковое пространство - это координатное пространство, в котором каждому комплексному числу a+bi+c соответствует точка М(а,b,c). Включает 1 действительную и 2 недействительные координатные оси (мнимую и глюковую). При b=c=0 z имеет действительное значение, при a=c=0 - мнимое, при a=b=0 - глюковое.

4њ Некоторые свойства глюковых чисел:

1) ^.0=0

2) ^.=(1^.1)/(0^.0)=1/0=

3) / =(1/0)/(1/0)=(1/0)^.0= ^.0=0

4) sqr( ) =

5) sqr( -) = sqr( ) ^.sqr(-1) = ^.i, где i - мнимая единица

5њ Общая ТЧК включает также понятие о гиперглюковых числах. Из свойства 5) глюковых чисел следует, что существуют числа, которым нет эквивалентных точек в глюковом пространстве. Числа d^{. .}i, где d - самое обыкновенное, примитивное, действительное число. Это мнимые глюки, либо гиперглюковые числа.

6њ Покажем, что других недействительных числовых множеств нет. Согласно ТЧК, общий вид любого числа: z = Asqr( 1/1)+Bsqr(1/0)+Csqr( -1/0)+Dsqr(-1/1)

Таким образом, с введением гиперглюковых исчерпываются все сочетания единиц, минус единиц и нулей в подкоренных выражениях. Любое перемножение участков приведенного числа не даст новых множеств.

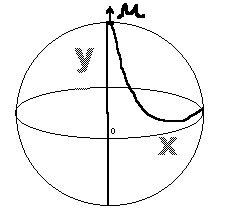
7њ Механическое объяснение существования глюковых чисел. Рассмотрим функцию f (x)=а/x. При x-> 0, f (x)->oo , т.е. точка M=f (x) разгоняется на бесконечность, с бесконечно возрастающим ускорением. На бесконечности (при x=0,f(х)=а) М обладает некоторой тангенциальной скоростью по отношению к координатной плоскости (поскольку плоскость - это сфера бесконечно большого радиуса и только на бесконечности можно обнаружить кривизну плоскости). Т.к. точка координатной плоскости не имеет массы, то на нее не действует никакой силы в сторону центра плоскости, а сила, сообщающая ей тангенциальное ускорение, не является ньютоновской. Таким образом, имея тангеницальный импульс (ведь у нее только масса покоя равна нулю), М покидает координатную плоскость и уходит в пространство. За абсциссу выберем действительную ось, а за ординату - мнимую, и М улетит в глюковое пространство.

Аналогично для гиперглюковых чисел, только они переходят в гиперпространство.

Примечание. Покинувшая плоскость точка занимает в пространстве положение, в зависимости о величины параметра а. Поскольку ее импульс пропорционален а, и ее движение замедляется под действием сил сопротивления математического вакуума, из которого, как известно, состоит пространство. В этом, к примеру, состоит различие между точками 2 и 3 .

Для любителей подумать
1. Не кажется ли вам, что из свойства 4.4њ .2) следует, что либо=1, либо =0? Ответ тут.

5. Теория точек (ТТ)

1њ Теория точек - это инструмент туфтологии, служащий для сведения науки к точке (2.3њ ). Здесь вселенная будет сведена к точке одним из методов, а именно, исходя из эквивалентности прямой и окружности бесконечного радиуса. Все теоремы доказаны для плоскости, но справедливы также и в пространстве.

2њ Две параллельные прямые могут пересекаться. На рисунке 3. две прямые а и b - параллельны, но имеют на бесконечности две точки пересечения А и В. Центр прямой b лежит внутри прямой а и их радиусы равны. Легко доказать, что такие прямые-окружности пересекаются.

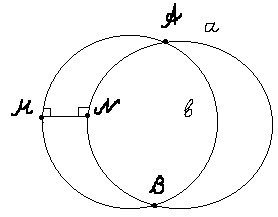
3њ Пересекающиеся прямые имеют две точки пересечения. Пусть прямые a и b пересекаются в точке А под некоторым углом (рис. 3). Тогда они имеют на бесконечности еще одну общую точку В, т.к. окружность (как и прямая) есть замкнутая линия.

4њ В плоскости существует только одна прямая. Действительно, если любые пересекающиеся прямые имеют две общие точки, то из аксиом планиметрии, они совпадают. Любая прямая, пересекающая одну из параллельных прямых, пересекает и другую, а значит, совпадает с обеими параллельными прямыми. А две прямые, совпадающие с третьей, также совпадают. Таким образом, все прямые в плоскости совпадают в одну, причем в любую из прямых, лежащих в этой плоскости.

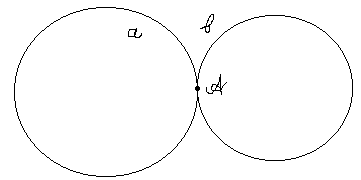
5њ Длины всех отрезков равны. Рассмотрим два отрезка АВ и MN. Оба они являются дугами окружностей равных (бесконечных) радиусов (R). Кроме того, оба отрезка имеют равную (стремящуюся к нулю) градусную меру (a). Длина дуги l_АВ=R^.a =l_MN, что и требовалось доказать.

6њ Две совпадающие прямые могут иметь только одну общую точку. Такой случай приведен на рис. 4. Две окружности бесконечного радиуса совпадают на бесконечном отрезке, но при стремлении к бесконечности, оказываются касательными друг к другу. А значит, по определению касающихся окружностей, имеют только одну общую точку.

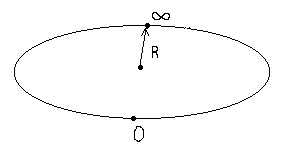
7њ Существует единственная точка и ничего кроме нее. Возьмем числовую прямую (рис. 5). Точка х=oo равноудалена от всех точек числовой прямой (окружности). Такие точки, как x=oo -dx=oo(при dx<>oo) совпадают с точкой бесконечность (в том числе точки, определенные как "соседняя с бесконечностью" и т.п.). Но геометрическое место точки, равноудаленной от всех точек окружности есть центр этой окружности. Значит х=oo лежит в центре числовой окружности и, одновременно, на окружности. Это возможно только в том случае, если радиус окружности R=0. Т.е. все точки прямой совпадают с точкой oo . И единственная прямая принадлежащая плоскости (см. 5.4њ ) состоит из одной точки, кроме которой ничего нет. Но существование этой точки невозможно подтвердить, поскольку нет объекта относительно она существует, относительно которого можно проводить эксперименты, ведь все познается в сравнении. Таким образом, точка существует лишь из предположения, что что-либо существует. Но, с другой стороны, если кто-то сделал это предположение, значит он существовал...

Ответы на контрольные вопросы

1.1 Нет, загрузочные линии невидимые.

1.2 а) 0,3, если не учитывать, что до о. Вознесения нельзя добраться поездом, а Лазарев каждые 5 минут смотрел на портрет друга, переживая из-за ссоры. б) 366.

2.1 Необходимо разбить ее на 108 меньших наук, каждая из которых сведена к точке.

2.2 Геометрический: объединение тройки и ее осевой симметрии; механический: с периодом Т=80 мин совершает колебания координаты от ул.Видова до ост. Малая Земля (частный случай); химический: результат трепанации p-связи; туфтологический: бесконечность, поставленная "на попа".

2.3 Синус. С английского sin переводится как грех.

3.1 Вполне.

3.2 А вот так вот!

4.1 Да, но это только кажется.