Решения

1. При сравнении вершин от А до С по часовой стрелке, получаем для углов: А> В, а В> C, значит А> C. При сравнении вершин от А до С против часовой стрелки, получаем, А< D, а D< C, значит А< C. Но т.к. магнитная индукция имеет направление за плоскость рисунка, то по правилу буравчика, обход вершин должен быть совершен по часовой стрелке, а значит А>C.

2. После описанной операции, первый камертон становится грязнее второго. Следовательно, его чистота n₁<n ₂ чистоты второго камертона. Длина звуковой волны L₁=z /n ₁>z /n ₂=L₂, где z -скорость звуковой волны в вакууме (заполненном воздухом). Т.е. длина волны для грязного камертона больше. Примечание. Это, кроме шуток, так, несмотря на то, что чистота - вещь относительная.

3. По определению натурального логарифма:

lnx = Integr(дx/x) = т дx^{.x -1}

По определению интеграла степенной функции, т x^{n .} дx = xⁿ⁺¹/(n+1)+c. Значит

lnx = x⁰/0-1/0 = x⁰ - = - =0, для x из R.

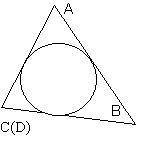
4. Любой треугольник одновременно является трапецией с одним из оснований равным нулю. Например, треугольник ABC на рис. 12 можно представить как трапецию ABCD, СD=0. В любой треугольник можно вписать окружность, значит полученная трапеция является описанной, но для каждой описанной трапеции верно равенство: AB+CD=AC+BD. Т.к. CD=0, а BD=BC равенство приобретает вид: АС+ВС=АВ.

5. Рассматриваемое множество точек образует икс в квадрате (букву "икс", находящуюся в квадрате). А известно, что "икс в квадрате" - это функция. Значит множество точек является графиком функции x^2.

6. Заменим охапку соломы эквивалентной пружиной некоторой жесткости k. Пусть D t - оптимальное время, за которое должно произойти поглощение энергии падающего на солому без ущерба для него. Обозначим за W энергию тела в момент столкновения с соломой. W зависит от, высоты h, с которой падает человек и его массы m. Изменение импульса человека за dt равно р=W/sqr(2gh) = F_срdt, Fср- среднее значение силы Гука. Отсюда следует, что с увеличением h или m необходимо увеличить k. В противном случае, увеличится dx - деформация соломы и потребуется большее ее количество, что нерационально. Значит, чем тяжелее человек, который падает на солому и чем с большей высоты он падает, тем больше жесткость соломы и тем меньше ее надо подстилать, чтобы она была пожестче. Да, физика соломы непостижима! Отметим, что в решении человек принят за материальную точку, что является либо сущей правдой, либо абсолютной истиной.

7. Необходимо получить вещество H₂O-OH. В нем валентность первого атома кислорода III. Но для нормального кислорода валентность II. Получим ненормальный кислород, т.е. свихнем нормальный.

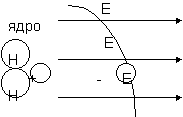
Поместим в сосуд с электродами некоторый объем кислорода. Затем, на долю секунды подадим напряжение на электроды. Рассмотрим отдельный атом кислорода. Для половины из них расположение ближайшего к ядру электрона, ядра и направление силовых линий поля будет таким, как показано на рис. 13, а для половины - обратным. Будем работать с первой половиной. Под действием электрической силы, ближайший электрон будет смещаться в сторону ядра, а ядро, имеющее положительный заряд, - в сторону электрона. Напряженность поля должна быть не менее нескольких гиганьютонов на нанокулон, поскольку электрон имеет пакостное свойство двигаться очень быстро и поле будет равные промежутки времени приближать и отдалять его от ядра. Одновременно кислород в сосуде подвергается бомбардировке электронными антинейтрино. Электрон, приблизившийся к ядру вплотную, один из протонов ядра, ближний к электрону и пролетающее мимо нейтрино создают новый нейтрон. Таким образом, масса ядра увеличивается, а внешняя оболочка лишается одного электрона, приобретая валентность III. Далее полученный кислород (III) реагирует с двумя атомами водорода и гидроксильной группой, ч.т.п. (что и требовалось получить).

8. Используем метод математической индукции. Докажем, что для nО Z, 2n+1 кратно 2.

1) проверим для n=0. 2n+1=n(2+1/n)=0(2+1/0)=0^.2+0= 0 - кратно 2.

2) предположим, что для n=k, 2k+1 кратно 2.

3) Докажем, что для n=k+1, 2(k+1)+1 кратно 2. 2(k+1)+1=(2k+1)+2. Оба слагаемых кратны 2, значит и сумма также кратна 2. Утверждение верно для n=k+1, значит и для любого n.

9. Найдем массу покоя рояля. Она складывается из массы покоя всех частиц, из которых рояль состоит. M=m_e^.10,52^.10²⁸+ m_p^.10,52^.10²⁸+m_n^.20^.10²⁷=210 кг.

Поскольку рояли тонут в воде, то их водоизмещение, в соответствии с законом Архимеда, равно их объему. Т.к. рояль носит марку "Красный Октябрь", то он изготовлен на одноименной фабрике. Но фабрика "Красный октябрь" выпускает исключительно шоколад, значит и рояль также выполнен из шоколада, потому что как же еще? Плотность шоколада равна r =M/V=420 кг/м^3.

10. Рассмотрим нотную запись "Контрреволюционного этюда". Вначале стоит значок рр (pianissimo или очень тихо). Он означает, что пианист давит на клавиши с силой, равной квадрату его веса (Р^.Р). Этюд состоит из 60 тактов, размер 4/4 и исполняется с частотой w =120 четвертных в минуту. Но! в этюде присутствуют паузы в количестве 17 четвертных. В это время сила не действует. Таким образом, на систему массой M=210+65 (кг) в течение времени T=(4^.60-17)/120 (мин) действует сила F=(60^.9,8)2(н). Скорость системы равна 164857 м/с. Что можно сказать? Музыка - великая стихия, могущественное искусство. Теперь по поводу вопроса задачи. Первая комическая скорость - это скорость, достаточная телу для выхода на орбиту Земли. Но т.к. опора невесомая, то ей любой скорости достаточно для выхода на орбиту.

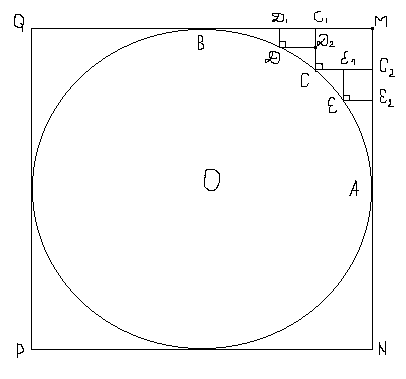
11. а) Пусть дан квадрат MNPQ, описанный около окружности О. Рассмотрим дугу АВ, ограниченную точками касания квадрата и окружности (см. рис.). С - середина И АВ. Опустим из С перпендикуляры на MQ и MN. С₁ и С₂ - концы перпендикуляров. Ломаная BC₁CC₂A равна по длине ломаной ВМА. Из середин И ВС и И СА, точек D и E повторим описанную операцию. Очевидно, что длина ломаной BD₁DD₂CE₁EE₂A также равна длине ВМА. 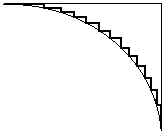Продолжая разбиения дуг и нахождения новой ломаной, равной по длине ВМА некоторое число раз, видим, что длина этой ломаной приближается к длине дуги АВ (рис. 15). При бесконечном числе разбиений, ломаная сливается с И АВ, т.е. является равной ей по длине. Отсюда L_АВ=L_BMA. Для всего квадрата получаем, что длина окружности равна периметру квадрата.
4а=2pi R. (1)

а=2Rtg45њ = 2R. Из (1) можно вычислить число p с точностью до десятых: p =4,0000000000 - десятая.
Равенство (1) верно также для n-угольника. na=2p R; p =n^.tg(180њ /n)
б) p =5^.tg36њ ~= 38,7524. в) p =6^.tg(180њ /6)=2sqr(3)

12. Указание. Попробуйте применить формулу бинома Ньютона, хотя вряд ли поможет.

13. Ответ: Все, что останется от декана - это горстка простейших углеводородов. Решение. Любой декан имеет молекулярную формулу С₁₀Н₂₂. В процессе термического крекинга, который как раз и происходит в ректификационных колоннах, декан может изомеризироваться (или иромеризовываться), в результате чего образуются вещества вроде 2-метилнонана или 3-этилоктана. Также может происходить распад декана на более легкие углеводороды и их изомеры (метан, этан, ацетилен, бензол и др.).

14. Исходя из принципа: одна голова хорошо, а две - лучше заключаем, что двуглавые - доминантные, а одноглавые - рецессивные. И первый закон Менделя тут совершенно ни при чем.

15. КПД селекции это, по всей видимости, отношение числа нужных орлов, к общему числу выведенных. Из условия видно, что никому не нужны любые орлы, кроме двуглавых. Обозначим их число как 2^-2.k. Тогда количество всех орлов равно 1/2^.k/(1-1/2)=k. КПД равен 1/4. Задача приобретает нездоровый смысл, т.к. n->oo. Ведь если получен хотя бы один бесконечноглавый орел, то число двуглавых равно бесконечности.

16. Задача имеет нездоровый смысл, аналогичный аналогичному смыслу задачи N 15. Вначале говорится, что M>>m, т.е. M:=m+dM, но с другой стороны m:=M:=m+dM - GOTO предыдущая строчка. Решение приобретает характер сказки про белого бычка и заканчивается, когда m и M становятся равными бесконечности. А поскольку тела имеют конечную скорость и выделяется конечная часть энергии данных в задаче предметов разной степени неупругости, а любая конечная часть от бесконечности равна бесконечности, то выделится бесконечная энергия.

17. Воспользуемся результатом решения задачи N 11. Возьмем окружность w ₁ длиной L₁₌₃Ц 3 и окружность w₂ длиной L₂=4. Около w ₁ опишем треугольник, тогда для w ₁ p = 3Ц 3, а около w ₂ опишем квадрат, и для w₂ p =4. R₁=L₁/2p =0,5, R₂=L₂/2p =0,5. R₁=R₂ при L₁? L_2.

18. U=0. На рис. 16 показан путь зарядов от А к В. Страшная была схема. Если у вас получился другой результат, то вы, вероятно, применяли правила Кирхгофа, законы параллельного-последовательного соединений, закон Ома, а может и Джоуля-Ленца. На самом деле, надо было применить голову. Но это совсем не очевидно, поскольку голову нужно применять, пожалуй, только в одной этой задаче из всего сборника.

19. Да, токи в обоих соединениях одинаковы и равны бесконечности. Но посмотрим на проблему в свете теории числовых комплексов. Токи равны I₁₌e₁/0=4 , I₂=e₂/0=7 . I₁-I₂=(4-7) =-3 , т.е. I₁<I_2.

20. 1) Проверим для 1 точки. Через одну точку проходит прямая.

2) Допустим, что через любые n точек проходит прямая.

3) Докажем, что через n+1 точку также проходит прямая. Выберем из n+1 точки какие-то n. По предположению индукции, через них проходит прямая а. Далее, выберем из n+1 n точек, в число которых входит ранее исключенная. Через них проходит прямая b. а и b имеют больше одной общей точки, т.е. совпадают.

21. Указание. Прыжок с парашюта, в отличие от прыжка с парашютом, можно считать свободным падением. Существует лишь одно исключение. А если, вдруг, самолет пролетал над Джомолунгмой или, например, над Эверестом? Высота этих гор как раз равна 8848 м. Но это не утешение, поскольку там воздуха мало, и протянет бедняга минут 10, от силы 20.

22. Спин электрона в единицах h равен 1, как и спин протона, нейтрона и нейтрино. Таким образом, спины этих частиц равны (одинаковы), и если их всех поставить спинами вперед, т.е. рассматривать сзади, то различий не обнаружится.

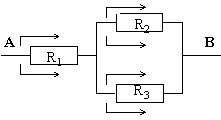
23. Напрасно вы забыли про сопротивление проводов. Ведь это единственные элементы схемы, обладающие сопротивлением, и вообще, единственные элементы схемы. Помимо того, что приведенная система не имеет решений, R₁, R₂, R₃ - не резисторы, а параллельные соединения проводов (рис. 17), а буквы R₁, R₂, R₃ написаны просто так, для развлечения. Ток равен бесконечности, если можно говорить о токе через несуществующие объекты.

24. а) Выберем на прямой а произвольные точки А и В. Очевидно, что в пространстве существуют вектора, неколинеарные вектору АВ, в то время как вектор, имеющий начало и конец в множестве точек, из которых состоит точка, нулевой вектор, колинеарен любому вектору пространства. Налицо факт, что нулевой вектор - это общий вид вектора, а значит прямая - частный случай точки.

б) Ромб - это разновидность квадрата, которому дали по шее.

25. Здесь парадокса нет. Пусть М=Х-х>>х. Тогда для М также верна теорема Синуса: М-х>>х. Производя вычитания х из Х [Х/х+1] раз, получим число М_k очевидно меньшее х, в то же время намного большее х по теореме Синуса, что удовлетворяет ОНТ.

26. Пусть а - некоторое действительное число. а=а+i-i, где i - мнимая единица. Рассмотрим слагаемое -i. (-i)=(-1)sqrt( -1). Внесем (-1) под корень. -i=(-1)sqrt( -1)=sqrt[ (-1)²(-1)]=sqrt( -1)=i. Тогда а=а+i+i=a+2i.

27. Ответ:(0;4). Найдем ОДЗ уравнения. Уравнение y²-8y=x-16 равносильно уравнению:
(y2-8y)¹=(x-16)¹. х и у должны удовлетворять двум совокупностям х-16>= 0; х-16<0 и y²-8y?>=0; y²-8y<0. Похоже, что х из R, у из R. Рассмотрим п.ч. уравнения: x-16=(i-i+1)x-16. Из решения задачи 26, (i-i+1)x-16=2ix+x-16. Т.к. y принадлежит R, то л.ч. имеет действительное значение. П.ч. имеет действительное значение только при х=0. Подставим х=0 в первоначальное. y²-8y=-16; (у-4)²=0, у=4.

28. Белые имеют беспроигрышную стратегию, заключающуюся в произвольной игре. Ведь шашка С1 стоит на белом поле и не может быть съедена.

29. Ферзь С5:С6 - Король Е8:Е7, Ферзь С6:С5 - Король Е7:Е8. Процедуру повторить 8 раз. 33-ий ход - Ферзь С5:Е5 - мат.

30. Директриса - прямая, лежащая в плоскости конического сечения (эллипса, гиперболы или параболы) и обладающая тем свойством, что отношение расстояний от любой точки кривой до фокуса кривой к расстоянию от той же точки до этой прямой есть постоянная величина (из МЭ). А углы пополам делит биссектриса. У директрисы для этого мало образования, ведь чтобы делить углы пополам, нужно знать, по меньшей мере, теорему о биссектрисе.

31. Возьмем отношение токов I₁/I₂=4 /7 =4/7(/). По свойству 4.4њ .3) / =0. Значит отношение двух ненулевых величин равно нулю, что невозможно.

32. Необходимо подвергнуть воду дегидратации. Дегидратация - это отщепление воды от какого-либо соединения.

33. В черном ящике находится магнитная лента. Вероятно, обгоревшая и порванная, так что ничего разобрать на ней невозможно. Внешним видом напоминает график функции Дирихле.

34. Указание. Прочитайте условие задачи N 38.

35. x²+5zcosy+ylog₂x+2zy=0, Уравнение равносильно системе:

x²+5zk+ym+2zy=0,

k=cosy,

m=log₂x. Произведем преобразования системы:

2^2m + 5zk + marccosk + 2zarccosk=0

2^m=x

y=+ arccosk. Полученную систему сведем к следующему уравнению:

2^2m+5zcosy+y(m+2z)=0, где m=log₂x

2²log2x +5zcosy+ylog₂x+2z=0, откуда

x²+5zcosy+ylog₂x+2zy=0 - такое уравнение мы уже умеем решать сведением к системе (см. выше). При решении использован модифицированный метод сведения к предыдущему. Модификация состоит в том, что сводят не к предыдущему, а к первоначальному.

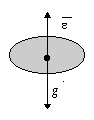
36. Угловое ускорение вращения пропеллера, в соответствии с правилом левого винта направлено вверх и равно e =w ', где w -угловая скорость. Поскольку w =const, w '=0 и e =0. Запишем результирующую силу, действующую на Карлсона во время полета, в проекции на вертикальную ось (рис. 18): S F=F₁-mg, где F₁- подъемная сила, обусловленная вращением винта. F1=me , поскольку других ускорений направленных положительно Карлсон не имеет. Значит S F=-mg. Ответ: Карлсону не повезет.

37. 1 способ: 2H₂+O₂-> 2H₂O_,

2 способ: 4H₂+2O₂-> 4H₂O_,

3 способ: 6H2+3O₂-> 6H₂O_{,
............................................}

n способ: (2n)H₂+(n)O₂-> (2n)H₂O

38. Указание. Для начала ознакомьтесь с условием задачи N 34.

39. Очередной раз воспользуемся утверждением, что треугольник- есть трапеция с нулевым основанием. Легко видеть, что окружность можно описать только около равнобедренной трапеции (рис. 19). Ее частный случай - равнобедренный треугольник (и никакой другой). Значит любой другой треугольник, являющийся частным случаем неравнобедренной трапеции, вписать в окружность нельзя, поскольку нельзя вписать никакую трапецию, кроме равнобедренной.