 (**),
(**),Этот доклад не звучал на конференции, но был написан специально для нее. Публикуется в память об Анатолии Павловиче.
А. П. Савин, кафедра высшей математики
Об одной гипотезе Ферма
Речь здесь пойдет, конечно же, о Великой теореме Ферма. Остальные гипотезы Пьера Ферма либо оказывались неверными, как, например, гипотеза, что все числа вида 22n+1 - простые, либо малоинтересными.
Промелькнувшее недавно сообщение о доказательстве Великой теоремы Ферма английским математиком Эндрю Уальсом не снижает интереса к этой задаче. Напомним, что теорема формулируется так: "При всех целых n>3 не существует натуральных чисел a, b и c, удовлетворяющих уравнению
an+bn=cn (*)"
Дело в том, что доказательство Э. Уальса содержит около 500 страниц текста, в то время как Пьер Ферма писал об удивительном доказательстве, для записи которого поля книги Диофанта оказались немного узкими.
Подобных доказательств придумано великое множество. Этот доклад имеет обзорный характер. Самые простые изящные доказательства, которые были независимо придуманы в разное время разными людьми, могут быть записаны следующим образом:
"Еще Пифагор доказал, что a2+b2=c2 (сумма квадратов катетов равна квадрату гипотенузы). Докажем, что an+bn <> cn, если n>3. Действительно, c>a и c>b
Если разделим обе части уравнения (*) на cn, то получим, что
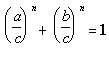 (**),
(**),
но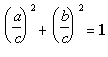
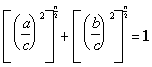
Но при возведении чисел, меньших 1, в степень, большую 1, получаются меньшие числа, следовательно, уравнение (**), как и уравнение (*), не может выполняться."
Можно привести много столь же коротких и простых доказательств, авторами которых являются люди разных возрастов, профессий и уровней образования - от школьников до заведующих кафедрами математики. Однако, недавно было обнаружено, что Великая Теорема Ферма формулируется совсем не так, как мы привели выше.
Дело в том, что во времена Ферма еще не было установившейся формы для записи алгебраических уравнений. То, что было написано Пьером Ферма, на самом деле в современной записи нужно записать в виде
na+nb=nc (***)
Доказательство того, что при n>2 это уравнение не имеет решений не представляет труда. Сократив на na (считаем, что a<>b), получаем 1+nb-a=nc-a.
Правая часть делится на n, а левая - нет. Единственное решение получаем при n=2 и a=b. В этом случае 2=2c-a, откуда c=a+1 и мы имеем верное равенство 2a+2a=2a+1.
Вернемся все-таки к наиболее распространенному варианту Великой Теоремы Ферма.
Многочисленные доказательства (*) основаны на чрезвычайно остроумном приеме: перенести bn в правую часть уравнения. Известна телеграмма в адрес Математического института Академии Наук, состоящая из следующей фразы:
Решил теорему Ферма зпт bn перенести в правую часть зпт подробности письмом тчк
Авторы этих доказательств используют свойства бинома, открытые И. Ньютоном. Однако Ферма умер в год окончания Ньютоном Кэмбриджского Университета и не мог поэтому использовать формулу бинома в своем доказательстве. Поэтому с точки зрения восстановления исторической правды эти весьма многочисленные доказательства являются как бы доказательствами второго сорта.
Из последних поступлений доказательств Великой Теоремы Ферма остановлюсь на кратких и ярких доказательствах А. М. Ветрова из г. Пензы. Вот одно из них:
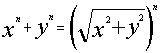 - абсурд,
следовательно, теорема доказана.
- абсурд,
следовательно, теорема доказана.
Мы не приводим здесь длинных доказательств, в которых многочисленные выкладки мешают педантам от математики находить не совсем доказанные места. Отмечу лишь одно из доказательств, которое позволило абитуриенту поступить на ФОПФ, имея по всем экзаменам тройки.
Во время собеседования он на пальцах доказал комиссии Великую Теорему Ферма, использовав следующий очевидный факт: все решения уравнения x2+y2=z2 описываются тройками вида (3k, 4k, 5k). Члены комиссии по собеседованию не смогли опровергнуть доказательства и абитуриент был принят в МФТИ.
Примечание вебмастера: Позволю себе привести тривиальное опровержение Великой Теормы Ферма. Перепишем (*) в виде:
a(n)+b(n)=c(n)
Таким образом, приходим к очевидному тождеству для любых n - равенство нулю производных n-ного порядка от констант.